Der Biegewellenwandler
Ein Lautsprecherprinzip
Klicken Sie HIER für eine Hörprobe meines Biegewellenwandlers aus Eigenentwicklung


Maturitätsarbeit von Matthias D. Kern
Klasse 6dG, 8. Dezember 2020
Lukas Morf (Betreuung)
Jürg Rüthi (Zweitbeurteilung)
1. Zusammenfassung
Meine Maturitätsarbeit «Der Biegewellenwandler – ein Lautsprecherprinzip» befasst sich mit der Frage, warum die Bauform des Biegewellenwandlers in der Lautsprechertechnik so wenig verbreitet ist. Die Antwort darauf suche ich nicht bloss in dicken Physikbüchern, sondern auch durch eine technische Produktion.
Im ersten Teil der Arbeit werden physikalische Grundlagen geschaffen, welche die Entwicklung eines Biegewellenwandlers ermöglichen. Danach wird ein Einblick in die aktuellen Anwendungen dieser Technik geboten, bevor ein drittes Kapitel sich der technischen Produktion widmet und diese anschliessend messtechnisch auswertet. Das abschliessende Fazit versucht, die Frage nach den Vor- und Nachteilen der Biegewellenwandler zu klären.
2. Vorwort
Bereits als meine Maturitätsarbeit noch in weiter Ferne lag, übten Lautsprecher eine grosse Faszination auf mich aus, denn ich hatte bis dahin aus Chassis der Firma VISATON und mithilfe deren Software Boxsim eigene Hi-Fi-Lautsprecher entwickelt und gebaut. Das reichte mir nun nicht mehr: Ich wollte wissen, ob ich einen Lautsprecher von Grund auf selbst konstruieren könne. Als die Themenwahl für die Abschlussarbeit anstand, entschied ich mich deshalb dazu, der technischen Produktion eines Biegewellenwandlers nachzugehen. Dieser Lautsprechertyp hatte meine Aufmerksamkeit gewonnen, da er zwar wenig verbreitet, aber vergleichsweise kostengünstig in der Herstellung ist. Ich stellte mir die Frage, weshalb sich der Biegewellenwandler bisher nicht kommerziell hat durchsetzen können, und beschloss, mit der Herstellung eines solchen Wandlers die Antwort darauf zu suchen.
So stürzte ich mich in die mir bis dahin fremde Welt der Körperschallwellen und begann mit der nun vorliegenden Arbeit.
Matthias D. Kern
Winterthur, Dezember 2020
3. Inhaltsverzeichnis
6. Selbstbau eines Biegewellenwandlers
6.1. Konzeption und Entwicklung
6.2. Auswertung und Optimierung
4. Biegewellen
Viele akustische Ereignisse in unserer Umwelt finden ihren Ursprung in schwingenden Festkörpern. Solche Klänge vernehmen wir beispielsweise, wenn die Kirchglocken schlagen, Geräusche durch die Zimmerwand dringen oder jemand Gitarre spielt. (Cremer & Heckl, 1996, S. 1) Was unsere Ohren dabei wahrnehmen, heisst Luftschall, während Schwingungen in Feststoffen als Körperschall bezeichnet werden.
Der Beweis dafür, dass Festkörper Schall aufnehmen, leiten und abgeben können, ist schnell erbracht: Die meisten von uns haben als Kind wohl ein Schnurtelefon gebaut und damit telefoniert wie die Erwachsenen, ohne dabei die zugrundeliegende Physik zu hinterfragen. Wir regten damals mit unserer Stimme die Dose zu Schwingungen an, welche die Schnur zur zweiten Dose leitete, wo sie wiederum als Luftschall abgestrahlt wurden.
Direkten Körperschall spüren wir nur, wenn Schwingungen auf unsere Knochen übertragen werden; zum Beispiel, wenn wir auf ein Lineal beissen und dieses in Schwingung versetzen. Auch die eigene Stimme wird durch den Schädelknochen geleitet, darum nehmen wir sie u. a. auf Sprachnachrichten als fremd war, da wir dort nur die Luftschallkomponente hören. (Wikipedia, Knochenleitung, 2020)
Schall breitet sich in Gasen und Fluiden immer als Longitudinalwellen (Druckwellen) aus. In Feststoffen treten zusätzlich Transversalwellen auf, deren Amplitude normal zur Ausbreitungsrichtung steht. Solche Wellen kommen ausschliesslich in Feststoffen vor, da nur diese auf Verformung mit einem Druck reagieren. (Möser, 2015, S. 129) Die untenstehende Abbildung illustriert einige Wellenformen, wie sie in Platten auftreten können:
Schema 1, Verschiedene Wellenformen
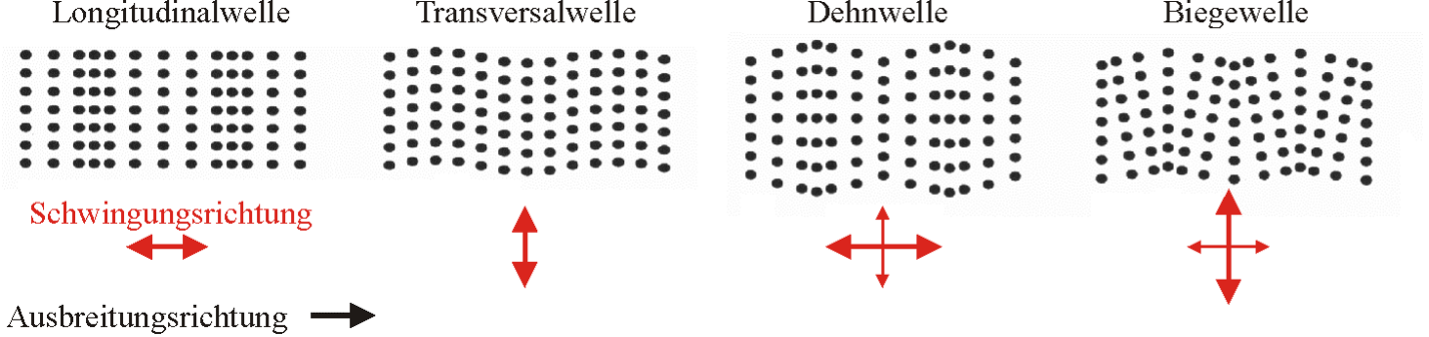
Von all diesen Wellenformen interessieren im Folgenden v. a. die Biegewellen, da diese durch ihre vergleichsweise grosse transversale Auslenkung am meisten Luftschall abstrahlen. (Möser, 2015, S. 131) Ausserdem können sie leicht angeregt werden – einerseits durch Luftschall, der auf einen Festkörper trifft (Schnurtelefon), andererseits durch mechanische Einwirkung (Klangschale).
Eine Platte kann also durch mechanische Anregung in Schwingung versetzt werden und macht die Frequenz der Anregung hörbar. Das kann man sich zunutze machen, um einen Lautsprecher umzusetzen, was das Ziel dieser Maturitätsarbeit ist. Für eine solche Konstruktion sind jedoch einige Eigenschaften der Abstrahlung von Biegewellen zu beachten, die nachfolgend präsentiert werden.
4.1. Koinzidenzfrequenz
Als Koinzidenzfrequenz wird eine wichtige Grösse in Zusammenhang mit Körperschall bezeichnet. Die Berechnung dieser Frequenz setzt einige nicht ganz triviale Zusammenhänge voraus, die in diesem Kapitel kurz aufgezeigt werden:
Die Luftschallgeschwindigkeit 𝑐 ist frequenzunabhängig und beträgt bei 20°C 343m/s. (Wikipedia, Schallgeschwindigkeit, 2020)
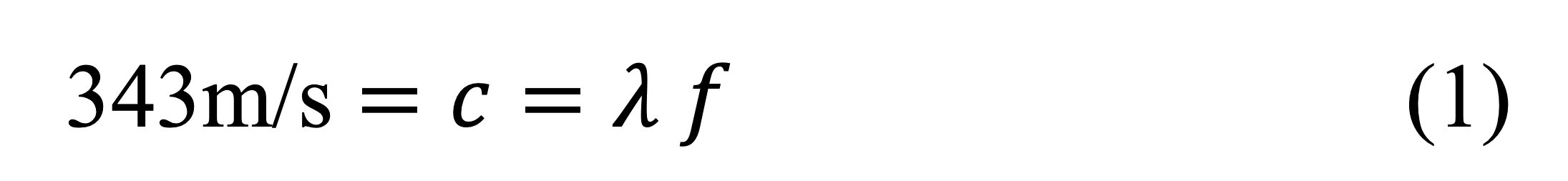
Hier steht 𝜆 für die Wellenlänge in Meter und für die Frequenz in Hertz (Hz). Bei einer Frequenz von 100Hz misst die Schallwelle also 3.43 Meter. Nun gilt die Schallgeschwindigkeit von 343m/s lediglich für Luft, bei anderen Gasen und Flüssigkeiten kann die Schallgeschwindigkeit wie folgt berechnet werden:

Dabei steht 𝑐0 für die Schallgeschwindigkeit im Medium, 𝐾 für dessen Kompressionsmodul[1] in Pascal und 𝜌 für die Dichte, die in kg/m3 angegeben wird. Für Wasser ergibt sich so die Rechnung:

1 «Er [der Kompressionsmodul] beschreibt, welche allseitige Druckänderung nötig ist, um eine bestimmte Volumenänderung hervorzurufen» (Wikipedia, Kompressionsmodul, 2020)
In Feststoffen ist eine generelle Berechnung der Schallgeschwindigkeit nicht möglich, da diese davon abhängt, ob es sich um Longitudinal- oder Transversalwellen handelt. Die longitudinale Ausbreitungsgeschwindigkeit 𝑐L lässt sich einem Material eindeutig zuordnen und wird mit Elastizitätskonstante 𝐸, Poissonzahl2 𝜐 und Dichte 𝜌 berechnet:

2 Die Poissonzahl – auch Querkontraktionszahl genannt – ist ein Zahlenwert, der die Volumenänderung eines Körpers bei Krafteinwirkung beschreibt. (Wikipedia, Poissonzahl, 2020)
Diese Gleichung ist jedoch äusserst ungünstig, da in vielen Tabellen mit Materialdaten die Poissonzahl fehlt. Eine gute Näherung lässt sich erreichen, wenn 𝜐 nullgesetzt wird. Dadurch wird zwar die Querkontraktion vernachlässigt, doch für viele Anwendung ist das ausreichend.
So erhält man:

Die transversale Ausbreitungsgeschwindigkeit 𝑐T ist hingegen von der Frequenz 𝑓 und der Materialdicke h abhängig, wie folgende Gleichung zeigt (Möser, 2015, S. 147):

Die transversale Ausbreitungsgeschwindigkeit gilt auch für Biegewellen, denn auch sie verhalten sich dispersiv, d.h. ihre Geschwindigkeit ist abhängig von der Frequenz.
Die Koinzidenzfrequenz teilt nun den Frequenzbereich des durch Biegewellen abgestrahlten Körperschalls in zwei Intervalle: Unterhalb dieser Frequenz ist die Biegewelle kürzer als die Luftschallwelle gleicher Frequenz, oberhalb ist sie länger. Folglich sind bei dieser Frequenz die transversalen Biegewellen gleich gross wie die Luftschallwellen. (Möser, 2015, S. 149 f.) Die Wellenlängen lassen sich aus den Gleichungen (1) und (1.4) berechnen. Wir können sie also gleichsetzen und nach der Frequenz auflösen. Daraus ergibt sich die Formel zur Berechnung der Koinzidenzfrequenz (Die Umformung finden interessierte Leserinnen und Leser im Anhang):

Ist die Biegewelle kürzer als die entsprechende Luftschallwelle, wird bloss ein «Biegewellennahfeld» abgestrahlt, das mit zunehmender Entfernung zur Fläche exponentiell abnimmt. Diese Tatsache rührt daher, dass der Abstrahlungswinkel 𝜑 vom Verhältnis zwischen den Längen der beiden Wellenformen abhängt. (Cremer & Heckl, 1996, S. 495)
Schema 2 veranschaulicht diesen Zusammenhang im Eindimensionalen, 𝜆0 steht im Nachfolgenden für die Länge der Luftschallwelle, 𝜆B für jene der Körperschallwelle:

Es wird deutlich, dass bei der Koinzidenzfrequenz der Abstrahlungswinkel maximal wird, da der Arkussinus von eins 90 Grad beträgt. Die Schallwellen dieser Frequenz breiten sich somit parallel zur Strahlerfläche aus. Anhand von Schema 2 lässt sich erkennen, dass die Luftschallwelle niemals grösser sein kann als die Biegewelle, folglich wird unterhalb der Koinzidenzfrequenz die Schallenergie nicht als Schallwellen abgestrahlt.
Die untenstehende Abbildung zeigt, wie die Schallenergie in einem Nahfeld nicht als eigentliche Schallwelle in die Luft abgegeben wird, sondern lediglich die Teilchen vor dem Strahler in Schwingung versetzt. Die Fortbewegungsrichtung der Biegewellen ist hier von links nach rechts:
Schema 2, Abstrahlungswinkel

Schema 3, Abstrahlung von Körperschall unter- resp. oberhalb der Koinzidenzfrequenz

Für einen Lautsprecher erscheint also eine tiefe Koinzidenzfrequenz (𝑓K) erstrebenswert. Nun soll das keinesfalls heissen, dass ein Lautsprecher mit einer hohen 𝑓K keine tiefen Töne anstrahlen könnte: Beispielweise operiert der Biegewellenwandler der deutschen Firma Manger ausschliesslich unterhalb seiner 𝑓K, die bei etwa 80kHz liegt (Hiebel, 2005, S. 95). Die Abstrahlung des Nahfelds wird nämlich überlagert von der nach unten zunehmenden Kolbenbewegung der schallabstrahlenden Fläche (bei Lautsprechern Membran genannt). Ein «reiner» Biegewellenwandler käme dementsprechend ausschliesslich oberhalb seiner 𝑓K zum Einsatz.
5. Der Biegewellenwandler
Seit Werner von Siemens 1878 den ersten elektrodynamischen Kolbenlautsprecher zum Patent angemeldet hat (Wikipedia, Lautsprecher, 2020), wurden zahlreiche Versuche unternommen, Schallwandler nach einem anderen Funktionsprinzip zu entwickeln. So existiert heute eine grosse Bandbreite unterschiedlicher Bauformen, doch durchgesetzt hat sich bislang keine gegen den Kolbenlautsprecher, der stetig weiterentwickelt wird. Die Thiele-Small-Parameter beispielsweise ermöglichen seit 1961 die physikalische Beschreibung eines solchen Lautsprechers nach dem Feder-Masse-Prinzip und sind für die Berechnung eines optimal abgestimmten Gehäuses unabdingbar (Wikipedia, Thiele-Small-Parameter, 2019). Der Biegewellenwandler verhält sich hingegen nicht nach dem Feder-Masse-Prinzip, weshalb diese Parameter nicht auf ihn anwendbar sind und in meiner Arbeit keine weitere Erwähnung finden werden.
Anders als bei herkömmlichen Schallwandlern bewegt sich beim Biegewellenwandler die schallabstrahlende Fläche nicht kolben- sondern wellenförmig. Sie wird durch einen elektromagnetischen Antrieb (vgl. 6.1.1) zu Biegewellen angeregt, die wiederum Schallenergie in die umgebende Luft abstrahlen.
5.1. Anwendungen
Seit langer Zeit fristen Biegewellenwandler ein Dasein abseits der kommerziell erfolgreichen Lautsprechertechnik. Bloss im Selbstbau-Sektor erfreuen sich viele Bastler an Konstruktionen mit sogenannten «Excitern», die an Platten befestigt werden, diese in Schwingung versetzen, und so die einfachste Form des Biegewellenwandler darstellen: Den «Distributed mode loudspeaker», auch DML-Panel genannt. Dabei wird eine (grosse) Platte zu Biegeschwingungen angeregt, wobei Resonanzen nicht gedämpft, sondern bewusst in Kauf genommen werden. Diese sollen möglichst weit über den Frequenzbereich verteilt auftreten (daher das «Distributed» im Namen) und so zu einer ausgeglichenen Wiedergabe führen. Solche Konstruktionen haben meist einen geringen Wirkungsgrad und eine schlechte Impulsantwort, weil die Platte – da ungedämpft – eine lange Ausschwingzeit aufweist. (Wikipedia, Distibuted mode loudspeaker, 2020)
In der Lautsprecherindustrie konnten sich Körperschallwandler nie durchsetzen, abgesehen von einigen Entwicklungen, die Kultstatus erlangten. Dazu zählt vor allem der Manger-Schallwandler; dieser sternförmige Lautsprecher ist wohl der bekannteste Biegewellenwandler überhaupt und besticht durch einen erstaunlichen Amplitudenfrequenzgang von 80-35’000 Hertz (Iris Strassacker Lautsprechershop). Anders als beim DML-Panel wird hier versucht, die Randreflexionen vollständig zu dämpfen, was sich in einer vorbildlichen Impulsantwort erkennbar macht.
In jüngster Vergangenheit scheinen plötzlich mehrere Hersteller von Unterhaltungselektronik Interesse an Konstruktionen mit Biegewellenwandlern zu zeigen: Sony verkauft Fernseher, deren Bildschirm als Lautsprecher fungiert unter dem Namen Sound-from-Picture-RealityTM (Sony, 2020). Auch in Mobiltelefonen ist eine ähnliche Technik anzutreffen, hier setzt beispielweise der Hersteller Google bei seinem Gerät Pixel 5 auf eine Hörmuschel, die im Display integriert ist und durch Anregung des hauchdünnen OLED-Panels funktioniert (PBKreviews, 2020). Diese Möglichkeit, Bildschirme als Lautsprecher zu nutzen, wird möglicherweise in Zukunft immer wichtiger werden; man denke nur an Vorteile wie absolute Wasser- und Schmutzfestigkeit eines solchen Schallwandlers.
6. Selbstbau eines Biegewellenwandlers
6.1. Konzeption und Entwicklung
6.1.1. Antrieb
Der Antrieb fast aller Lautsprecher beruht auf dem elektrodynamischen Prinzip. Dieses Funktionsprinzip wird hier nur oberflächlich behandelt, da es nicht nur beim Biegewandler zum Einsatz kommt und bereits Gegenstand unzähliger Abhandlungen ist. (Empfehlungen für weiterführende Literatur finden sich im Anhang.) Im Grunde handelt es sich beim elektrodynamischen Antrieb zumeist um eine Spule, die sich im Magnetfeld eines Dauermagneten (üblicherweise Ferrit- oder Neodym-Magnete; letztere haben eine höhere Energiedichte) befindet und von Wechselstrom durchflossen wird. Kolbenlautsprecher haben stets runde Magnete, ich aber war gezwungen, meine Spule mit Quadermagneten anzutreiben, denn solche konnte ich in gebrauchtem Zustand beziehen. Also entwarf ich einige Skizzen und testete mögliche Lösungen mit kleinen Neodym-Magneten, bis ich zu einem zufriedenstellenden Ergebnis gelangte und dieses mit grösseren Magneten umsetzte. Erst später stiess ich im Internet auf den Dänen Joppe Peelen, der auf seinem Youtube-Account einen Eigenbaulautsprecher mit einem ähnlichen Antrieb vorstellte. (Peelen, 2016)
Das Prinzip funktioniert folgendermassen: Zwei von insgesamt vier Quadermagneten werden jeweils zwischen zwei Eisenstangen geklemmt. Dadurch werden die Eisenstangen magnetisiert und können nun – bei entsprechender Anordnung – ein starkes Magnetfeld in einem schmalen Spalt zwischen sich hervorrufen, wo die Spule zu liegen kommt. Die nebenstehende Skizze illustriert den Aufbau von oben betrachtet, wobei Spule und Membran senkrecht auf der Ebene stehen.
In Schema 4 ist die Flussrichtung des Stroms in der Spule nicht zu erkennen, da es sich bei elektrischen Audiosignalen um Wechselstrom handelt. Das ist auch der Grund, warum die Lorentzkraft hier in zwei Richtungen wirkt. Die schwarzen Pfeile illustrieren das Magnetfeld zwischen den Eisenstangen.
Schema 4, Elektrodymamischer Antrieb im horizontalen Querschnitt

Bei der praktischen Umsetzung dieses Antriebsmechanismus stellten sich einige Hürden mir in den Weg; zunächst waren massive Eisenstangen der Abmessung 11×2.5×1.5cm schwieriger zu finden als gedacht, da die meisten Baumärkte heutzutage nur noch Aluminium und Hohlstangen verkaufen. Fündig wurde ich schliesslich in einer Schlosserei. Später gingen beim Hantieren mit den kräftigen Neodymmagneten zwei davon in die Brüche, da sie durch die starke gegenseitige Anziehung aneinanderprallten und durch die enorme Wucht beide zersplitterten. Das zeigt, welche Magnetkraft für solch einen Lautsprecher vonnöten ist.
Das Wickeln einer passenden Schwingspule für den maximalen Wirkungsgrad stellte eine weitere Herausforderung dar, da ich für mein Magnetsystem eine rechteckige und flache Spule benötigte. Die runden Spulen, von denen Konuslautsprecher angetrieben werden, sind wesentlich einfacher herzustellen, indem sie auf einen Spulenträger gewickelt werden, der in einem runden Magnetspalt zu liegen kommt. Auch ich musste ein geeignetes Material finden, auf dem ich meine Spule befestigen konnte, und meine Wahl fiel – nach Versuchen mit Karton und Aluminium – auf den Kunststoff PET. Die zwei zuerst getesteten Materialien weisen gegenüber dem Kunststoff entscheidende Nachteile auf: Karton ist relativ weich und absorbiert deswegen einen Teil der Energie, die von der Spule auf ihn übertragen wird, während Aluminium zu einem gewissen Grad magnetisch ist und deshalb vom Magnetsystem beeinflusst wird. (Aluminium gilt als paramagnetisch, weist also eine geringe Magnetisierbarkeit auf, die meist vernachlässigbar ist (Wikipedia, Aluminium, 2020). Die magnetische Feldstärke in meinem Antrieb ist jedoch genügend stark, dass sich dieser Effekt deutlich bemerkbar machte.)
Für die Schwingspule verwendete ich einen mit Lack isolierten Kupferdraht mit einem Durchmesser von 0.2mm. Den Widerstand R des Drahts lässt sich mit folgender Formel berechnen:

0,0171 ist dabei der spezifische Widerstand von Kupfer bei 20 Celsius, angegeben in .
Ich strebte für meinen Lautsprecher einen Gleichstromwiderstand von 4Ω an, was der Rechnung zufolge einer Drahtlänge von etwas mehr als 7m entspricht. Das Multimeter misst an der fertigen Spule 3.7Ω und bestätigt damit die Rechnung. Die 7m Draht wurden auf das PET-Plättchen gewickelt; jeweils 3.5m auf jeder Seite, damit die Schwingspule gleichmässig angeregt wird. Das Plättchen wurde mit Heissleim auf der Membran fixiert, hierbei war hohe Präzision gefordert.
Das fertige Antriebssystem ist auf den folgenden Aufnahmen abgebildet. Die elastischen Bänder am Magneten sorgen dafür, dass die Spule zentriert bleibt und nicht am Magneten kratzt. Die Flexibilität dieser Aufhängung muss gegeben sein, damit die Spule ungehindert auslenken kann.
Aufnahme 1, Schwingspule auf PET-Träger

Aufnahme 2, Magnetsystem mit Zentrierung

(Quelle: Eigene Aufnahmen, shot on iPhone SE 1st Gen.)
6.1.2. Membran
Das Kapitel 4.1 Koinzidenzfrequenz bietet die Grundlage zur Suche nach geeigneten Materialien für die Membran eines Biegewellenwandlers. Angestrebt wird ein breitbandiges Abstrahlverhalten, d.h. es sollen möglichst tiefe und möglichst hohe Frequenzen abgegeben werden können. Um dies zu erreichen, entschied ich mich für eine Kombination aus drei verschiedenen Holzplatten, die jeweils unterschiedliche Abmessungen und Koinzidenzfrequenzen aufweisen: Die mittlere ist eine 3mm starke Hartfaserplatte, die äusseren Platten bestehen aus Pappelsperrholz und haben eine Dicke von 6 resp. 12mm. Die ganze Membran hat die Abmessungen eines DIN A2 Papiers, da ich dessen Seitenverhältnis (1: ) für geeignet halte, um Plattenresonanzen zu verhindern. Die drei Holzplatten sind folgendermassen angeordnet:
Schema 5, Aufbau der Membran

Wie beim DML-Panel (vgl. 5.1 Anwendung) habe ich bei meiner Membran darauf geachtet, die Resonanzfrequenzen über das gesamte Frequenzspektrum zu verteilen. Daher ist auch die vertikale Positionierung der Schwingspule bewusst asymmetrisch. Die Koinzidenzfrequenzen der drei verwendeten Hölzer betragen nach Kapitel 1.1 (Koinzidenzfrequenz) 7980Hz für die Hartfaserplatte, 3591Hz für die dünnere Sperrholzplatte und 1796Hz für die dickere. Die Werte für diese Berechnungen entstammen dem Buch «Körperschall». (Cremer & Heckl, 1996, S. 147)
Die Schwingspule wurde möglichst exakt in einem rechten Winkel auf die Hartfaserplatte geleimt, höchste Genauigkeit war darum gefordert, weil der Magnetspalt bloss wenige Millimeter breit ist und ein Schaben der Spule gravierende Störgeräusche und Schäden am Kupferdraht zur Folge hätte. Diese Erfahrung musste ich machen, als ich die Membran einbaute und zu zentrieren versuchte. Restlos gelungen ist mir dieses Kunststück erst Monate nach dem ersten Anlauf, indem ich die Membran etwas drehte. So konnte ich die hörbaren Geräusche der Spule schliesslich beseitigen.
6.1.3. Gehäuse
Ein Lautsprecher braucht nicht zwingend ein Gehäuse. Beispielsweise DML-Panels (vgl. 5.1 Anwendung) kommen ohne ein solches aus, doch dieser Verzicht geht mit einem «akustischen Kurzschluss» einher: Bei tiefen Frequenzen findet zwischen Vorder- und Rückseite der schallabstrahlenden Fläche ein Druckausgleich statt, der dazu führt, dass zwar Luft bewegt, aber kein Schall abgestrahlt wird. (Hausdorf, 2013, S. 63 f.) Das äussert sich in einem bassarmen Klang.
Nun gibt es verschiedene Ansätze, wie sich dieser Kurzschluss verhindern lässt: Man könnte eine möglichst grosse Schallwand anstreben, die den Weg zwischen den Seiten vergrössert, oder man vernichtet den rückwärtigen Schall in einem geschlossenen Gehäuse. Für letztere Gehäuseform entschied ich mich schliesslich v.a. wegen der kompakten Grösse, die sich damit realisieren lässt. Der Vollständigkeit halber soll an dieser Stelle auf weitere Gehäuseformen aufmerksam gemacht werden; der rückwärtige Schall lässt sich nämlich auch umleiten und nutzen. Da er zum vorne abgestrahlten Schall einen Phasenversatz von 180 aufweist, muss dabei die Phase gedreht werden, das gelingt beispielsweise mit Transmissionline- und Bassreflexgehäusen.
Um in meinem geschlossenen Gehäuse Schallenergie zu absorbieren, setzte ich Dämpfwolle der Firma VISATON ein. Die Wolle soll die Schallwellen absorbieren und in Wärme umwandeln, was sogenannte «stehende Wellen» verhindert, die zwischen den Gehäusewänden entstehen würden.
Aufnahme 3, Gehäuse vor dem Einbau der Membran

Wichtig für eine gute Absorption ist der luftdichte Anschluss an die Membran, wofür eine zweck-entfremdete Türdichtung herhalten musste. Sie verhindert ausserdem ein Mitschwingen des Gehäuses und wurde unter die Membran geklebt, die von vier Schrauben in Position gehalten wird. Der Plattenrand wird auf die Dichtung gepresst, was Randreflexionen zwar dämpft, aber kaum verhindert.
Funktionale Erweiterungen wie Standfüsse und Tragegriff wurden ebenfalls am Gehäuse befestigt, beeinflussen aber das Wiedergabeverhalten des Lautsprechers nicht.
6.2. Auswertung und Optimierung
Als nach langen Abenden in der Werkstatt endlich ein funktionierender Biegewellenwandler vor mir stand, war ich verblüfft über die Lautstärke und Tiefe der Töne, die diesem Holzkasten zu entlocken waren. Nach einigen Tests mit verschiedenen Liedern fiel jedoch unangenehm auf, dass der Lautsprecher starke Verzerrungen aufwies, die bei einigen Frequenzen besonders zutage traten (vgl. Anhang). Mit dem Anzugsdrehmoment der vier Schrauben, von denen die Membran gehalten wird, versuchte ich, diese Verzerrungen zu eliminieren. Viele Stunden minutiöser Arbeit zeitigten jedoch nicht das erwünschte Resultat, was mich beinahe verzweifeln liess. Durch Zufall entdeckte ich, dass die störenden Geräusche nicht von der Membran, sondern von der Spule stammten, die am Magneten kratzte. Mit diesem Wissen gelang es schliesslich, die Membran neu auszurichten und damit eine zufriedenstellende Wiedergabetreue zu erreichen.
In der Folge zeigte sich bei zahlreichen Hörproben eine unerwartete Pegelfestigkeit einerseits, doch auch eine ernüchternde Wiedergabe der oberen Höhen (6’000-10’000Hz) andererseits. Zu erklären ist das wohl mit den Materialeigenschaften der Hartfaserplatte, die für diesen Frequenzbereich vorgesehen ist: Ihre Koinzidenzfrequenz liegt zwar im richtigen Bereich, doch vermutlich ist sie zu dick und somit zu träge für Anregung zu solch hochfrequenten Schwingungen. Ein Auswechseln der Holzplatte war nicht denkbar, also suchte ich eine andere Lösung, die ich in einer einfachen Konstruktion fand: Ein halbierter Pingpongball wurde mit einem konischen Stück PET über der Position der Schwingspule angebracht, um transversale Auslenkung direkt abzustrahlen. Es handelt sich also hierbei um einen einfachen Konuslautsprecher, den ich in den Biegewellenwandler integriert habe. Das scheint mir in Anbetracht der Wirkung legitim: Beispielsweise klingen Zischlaute der menschlichen Stimme nun viel präsenter und natürlicher. Der Lautsprecher in seiner finalen Form ist auf dem Titelbild zu sehen.
6.2.1. Frequenzgang
Das Klangbild würde ich als sehr plastisch beschreiben: Da die schallabstrahlende Fläche relativ gross ist, erzeugt der Biegewellenwandler eine gewisse Räumlichkeit; Instrumente wirken differenziert und klar gestaffelt. Im Besonderen werden perkussive Rhythmen mit grossen Dynamiksprüngen äusserst scharf umrissen in den Hörraum gezeichnet (beispielsweise in «Billie Jean» von Michael Jackson oder «Africa» von TOTO).
Diesen Höreindruck wollte ich mit einer messtechnischen Auswertung überprüfen. Um an professionelle Messinstrumente zu kommen, nahm ich also Kontakt zu einer Lautsprecherfirma auf, die mir jedoch eine Absage erteilte mit dem Verweis auf die geltenden Schutzmassnahmen infolge der COVID-19-Pandemie. Trotzdem wollte ich meinen Lautsprecher auswerten und entschied mich, ihn selbst einzumessen. Hierfür benutzte ich das Mikrophon «UMIK-1» der Firma MiniDSP und die Software REW («Room EQ Wizard»). Dieses Programm ist sehr benutzerfreundlich und es gelang mir damit schnell, erste Messungen vorzunehmen. Das UMIK-1 hatte jeweils einen Abstand von einem Meter zu der Membran und war auf den Pingpongball ausgerichtet. Das Mikrophon war mit der entsprechenden Datei des Herstellers kalibriert und der Biegewellenwandler stand in der Raummitte etwa einen Meter über Boden.
Die Messungen wurden jeweils mehrmals wiederholt, um Ungenauigkeiten auszuschliessen, doch sollten sie trotzdem mit Vorsicht genossen werden, da sie in einem Wohnzimmer resp. Keller aufgenommen wurden und der Nachhall im Raum sowie Hintergrundgeräusche die Ergebnisse verfälschen. Für eine Einschätzung des Lautsprechers sind sie jedoch mehr als ausreichend.
In Messung 1 ist der Frequenzgang grün und die Impedanzkurve rot eingezeichnet. Auf den grünen Graphen wurde für diese Darstellung eine Glättung von 1/6 Oktave angewendet.
Messung 1, Frequenzverlauf, gemessen mit UMIK-1
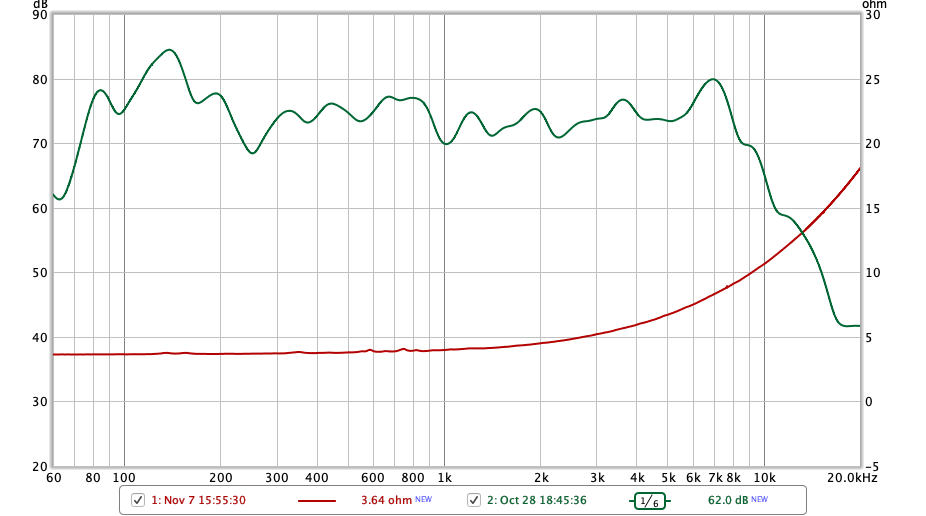
Der Frequenzgang zeigt, dass der Lautsprecher tatsächlich in einem grossen Frequenzspektrum linear ist: Zwischen 300 und 9’000 Hertz bewegt sich der Schalldruck in einem Bereich von 10 Dezibel (dB). Zum Vergleich: Das menschliche Gehör kann – abhängig von der Frequenz – erst einen Pegelunterschied von mehr als einem dB wahrnehmen. Die obere menschliche Hörschwelle sinkt im Laufe des Lebens von 20’000 auf ca. 16’000Hz. (Wikipedia, Hörfläche, 2020)
In der obigen Darstellung ist neben dem Frequenzgang auch der Impedanzverlauf abgebildet. Er zeigt den Widerstand in Ohm ( ) der Schwingspule in Abhängigkeit zur Frequenz. Diese Messung war ebenfalls mit REW möglich, jedoch musste der Lautsprecher zuvor wie folgt an die Soundkarte eines Computers angeschlossen werden:
Schema 6, Messvorrichtung für Impedanzverlauf

Der Widerstand Rsense wird bestimmt (hier: 101,8Ω ) und dient als Referenz für die Messung. Die Soundkarte kann nun die Spannungen messen, die an Widerstand und Lautsprecher anliegen. Da nach dem Ohm’schen Gesetz U1 : U2 = R1 : R2 gilt, kann REW vom bekannten Rsense auf den Widerstand des Lautsprechers schliessen. Diese Messung wird für alle Frequenzen bis 20’000Hz durchgeführt.
Daraus ergibt sich eine Kurve, mit der sich die Induktivität der Schwingspule berechnen lässt – angegeben in Henry (H). Die Software REW kann die Induktivität zwar berechnen, diese ist aber nicht ganz frequenzunabhängig: Beispielsweise können zusätzliche Wirbelströme auftreten, die den Scheinwiderstand zu hohen Frequenzen hin ansteigen lassen, indem sie dazu führen, dass der Kern des Leiters nicht mehr von Strom durchflossen wird. Bei sehr hohen Wechselstromfrequenzen (>107Hz) ist der Stromfluss lediglich auf die äusserste Schicht des Leiters reduziert, weshalb dieses Phänomen Skin-Effekt genannt wird (Hering, Martin, & Stohrer, 2004, S. 315).
Herstellerangaben für die Spuleninduktivität werden meist bei 1kHz gemessen, bei dieser Frequenz berechnet REW für meine Schwingspule 0.175mH. Dieser Wert ist nachvollziehbar; beispielsweise wird für den kleinen Breitbandlautsprecher FR10 der Firma VISATON ein Wert von 0.2mH genannt. (VISATON, 2019/2020, S. 365)
Eine weitere wichtige Komponente im Wiedergabeverhalten eines Lautsprechers ist der Verzerrungsgrad. Dieser Wert wird entweder als Klirrfaktor 𝑘 in % oder als Klirrdämpfungsmass in dB angegeben. Die beiden Einheiten gehen folgendermassen ineinander über:

Bis 150Hz ist ein Klirrfaktor über 5% hörbar, oberhalb dieser Frequenz bereits über 0.5%. Entsprechend liegt diese Hörschwelle bei einem Dämpfungsmass von 26 bzw. 46dB.
(Wikipedia, Klirrfaktor, 2020)
Messen kann man den Verzerrungsgrad ebenfalls mit REW. In der untenstehenden Grafik lässt sich der Frequenzgang (braun) ablesen und im Vergleich dazu ist schwarz die THD eingezeichnet, die «gesamte harmonische Verzerrung» (Wikipedia, Total Harmonic Distortion, 2019). Sie gibt Auskunft darüber, wie starke Störgeräusche der Lautsprecher bei der gemessenen Lautstärke produziert. Bei einem höheren Pegel wäre der Anteil der Verzerrungen bedeutend grösser, weil dann weitere Bereiche der Konstruktion zu schwingen beginnen. Auf der y-Achse liegt die Skala für den Verzerrungsgrad, hier als Klirrdämpfungsmass und darum in dB:
Messung 2, Verzerrungsgrad meines Lautsprechers
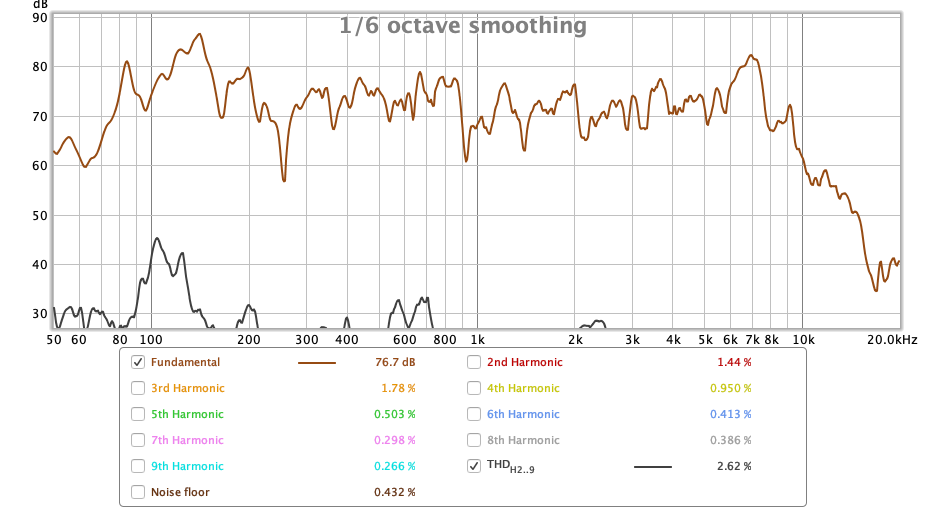
Die Kurve lässt sich nun folgendermassen ablesen: Wenn die THD von der Gesamtlautstärke subtrahiert wird, ist das Ergebnis das Dämpfungsmass. In dieser Messung liegt lediglich die Verzerrung um 600Hz im hörbaren Bereich. Nun lässt sich anhand dieser Grafik nicht bestimmen, was der Auslöser dieser kritischen Störgeräusche ist; neben dem Lautsprecher selbst könnte auch irgendein Gegenstand im Raum bei dieser Frequenz resonieren und somit das Geräusch hervorrufen. Um diese Unsicherheit auszuschliessen, wiederholte ich dieselbe Versuchsanordnung in einem anderen Zimmer, wobei sich das Resultat zwar vom ersten unterschied, die Verzerrungen bei 600Hz jedoch bestehen blieben. Es ist also davon auszugehen, dass sie konstruktionsbedingt sind.
6.2.2. Abstrahlverhalten
Nachdem nun Frequenzgang und Impedanzkurve bekannt sind, interessiert im Folgenden das Abstrahlverhalten unter Winkel. Es wird ermittelt, wie sich der Frequenzgang verändert, wenn das Messmikrophon (oder der Musikgeniesser) nicht mehr auf Achse, sondern in einem Winkel zur Membran steht. Für folgende Grafik wurden zwei Frequenzgänge gemessen: Das Mikrophon befand sich jeweils im Abstand von einem Meter zum Lautsprecher und war während der ersten Messung axial auf diesen gerichtet. Vor der zweiten Messung wurde der Biegewellenwandler um 30 nach links gedreht, für dieselbe Drehung in anderer Richtung ist ein ähnliches Ergebnis zu erwarten. Die Winkelmessung ist orange und die Achsenmessung grün dargestellt, beide Kurven sind geglättet:
Messung 3, Mein Lautsprecher unter Winkel

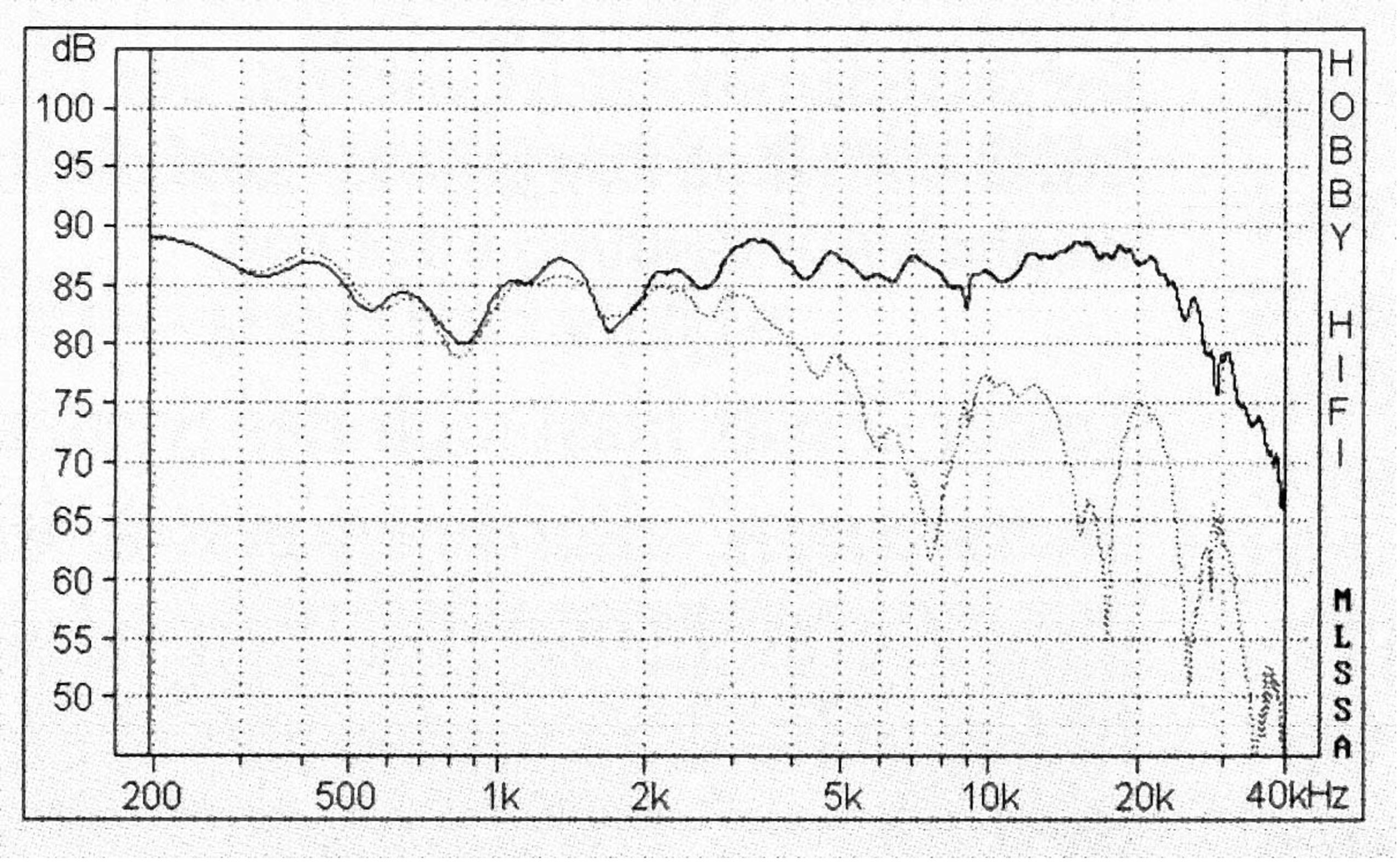
Es fällt auf, dass die Kurven kaum voneinander abweichen. Das ist erstaunlich, weil viele Lautsprecher dazu neigen, hohe Frequenzen sehr gebündelt abzustrahlen. Beispielsweise der bereits mehrfach erwähnte Manger-Schallwandler – ebenfalls ein Biegewellenwandler – zeigt zwar axial einen weitaus besseren Frequenzgang, aber unter 30 (punktiert) auch ein massiv stärkeres Bündelungsverhalten:
Messung 4, Manger-Schallwandler unter Winkel
7. Fazit
Zu Beginn dieser Arbeit wurde die Frage gestellt, warum ein solch vielversprechendes Lautsprecherprinzip nur wenig verbreitet ist. Nach vertiefter Auseinandersetzung mit dem Biegewellenwandler glaube ich, dass das Potenzial dieser Lautsprecher noch lange nicht ausgeschöpft ist: Zwar werden bereits einzelne Geräte mit schallabstrahlenden Displays verkauft, doch sind es noch wenige an der Zahl.
Ein entscheidender Vorteil von Konstruktionen mit Biegewellenwandlern ist der enorm breite Abstrahlwinkel, der damit erzielt werden kann. Das eröffnet Möglichkeiten in Bereichen, wo viele Menschen gleichzeitigt erreicht werden sollen, etwa in Kinos. Eine Idee wäre dort der Einsatz von Biegewellenwandlern als Surround-Lautsprecher, wobei hier vermutlich der verhältnismässig geringe Wirkungsgrad zum Problem würde: Für die Beschallung grosser Säle wäre wohl eine grosse Anzahl von Biegewellenwandlern nötig. Durch die preisgünstige Herstellung wäre ein solcher Aufbau dennoch umsetzbar.
Es sind auch Anwendungsbereiche denkbar, in denen der Schutz vor Natureinflüssen oder Vandalismus zentral ist; mir kämen da Lautsprecher für Zugdurchsagen oder sprechende Ticketautomaten in den Sinn. Auch kann ein solcher Lautsprecher optimal ins Design integriert werden, da die Membran – eingelassen in eine Wand – in der gleichen Farbe wie die Umgebung gestaltet werden könnte.
Für den Einsatz im Hi-Fi-Bereich sind Biegewellenwandler dagegen nur wenig geeignet. Die Messungen haben ergeben, dass der Frequenzgang eher wellig ist, da auslaufende Wellen nicht restlos gedämpft werden können und deshalb am Rand reflektiert werden. Diese Welligkeit tritt nicht nur bei meinem Exemplar auf, auch der mehrfach erwähnte Manger-Schallwandler hat einen eher unausgeglichenen Frequenzgang.
Vielleicht ist die grosse Zeit für den Biegewellenwandler jetzt gekommen, da flexible Display-Panels hergestellt werden können (man denke an faltbare Smartphones). Diese Panels haben vermutlich gute Eigenschaften, um als Lautsprecher genutzt werden zu können, da sie für eine Anregung zu Schwingungen genügend biegeweich sind. Vielleicht wird man schon in naher Zukunft im Alltag sehr viel häufiger einen Biegewellenwandler hören…
Nach dem Lesen dieser Arbeit muss man sich unweigerlich die Frage stellen, wie mein Biegewellenwandler denn nun tatsächlich klingt. Ein Frequenzverlauf ist ja schön und gut, aber eben bloss eine Linie… Aus diesem Grund möchte ich eine konkrete Impression ermöglichen: Der Link auf der Titelseite führt zu einer Aufnahme, wie mein Lautsprecher Alicia Keys’ «Underdog» spielt. (Anm. d. Verf.: Mit Kopfhörern erhält man einen sehr guten Höreindruck!)
Der Lautsprecher kann sich durchaus sehen – und vor allem hören – lassen. Sein Impedanzgang ist ebenfalls vorbildlich, weshalb Verstärker keinerlei Probleme damit haben. Perfekt ist mein Produkt aber bei weitem nicht; im Hochtonbereich fällt der Wirkungsgrad bereits unterhalb der Hörschwelle zusammen. Für eine Weiterentwicklung würde ich deshalb sicherlich ein dünneres Material für die mittlere Platte verwenden, in der Hoffnung, so eine Wiedergabe bis 20 kHz zu erreichen. Ausserdem könnte ein grösseres Gehäuse eine tiefere Abstimmung und damit einen volleren Klang bewirken. Nichtsdestoweniger bin ich äusserst zufrieden mit dem Ergebnis. Es darf schliesslich nicht vergessen werden, dass mein Biegewellenwandler den ganzen Wiedergabebereich alleine abdeckt, während in vielen kommerziell verfügbaren Lautsprecherboxen mehrere Treiber zum Einsatz kommen. Bei solchen Mehrwegeboxen wird der Frequenzbereich von einer Weiche auf die Treiber verteilt, damit diese nur Frequenzen wiedergeben müssen, für die sie spezialisiert sind; z.B. werden Hochtöner erst ab ca. 2kHz eingesetzt. (Hausdorf, 2013, S. 97)
Der finanzielle Aufwand für die Bauteile, welche für diese Arbeit gekauft wurden, hielt sich in Grenzen:
- Holz: CHF 20
- Kupferdraht 0.2mm: CHF 2,85 (für 113m, benutzt wurden 7m)
- Magnete: CHF 25 (für 6 Stk., benutzt wurden 4)
- Türdichtung: CHF 33 (verbaut wurde nicht einmal ein Viertel)
- Eisenstangen: CHF 5
Kleinere Dinge wie Kabel, Wolle oder Anschlussstecker waren bereits vorhanden, hätten aber den Gesamtpreis nicht in die Höhe getrieben. Dieser liegt unter CHF 90.
Natürlich muss auch der Zeitaufwand berücksichtigt werden, den ich für das Herstellen meines Biegewellenwandlers betrieben habe. Das eigentliche Zusammenbauen war innerhalb einer Herbstferienwoche erledigt, viel länger dauerte dafür das Einlesen und die Planung. Und ganz ohne Vorwissen im Bereich der Akustik wäre das Projekt wohl nicht gelungen.
8. Schlusswort
Es ist ein gutes Gefühl, ein Schlusswort zu schreiben. Ich schaue zurück auf eine intensive Arbeitsphase, in der ich unglaublich viel gelernt habe. Das Gelingen des Biegewellenwandlers war nicht nur einmal infrage gestellt, doch immer eröffnete sich eine Lösung für das Problem.
Die folgenden Zeilen möchte ich nutzen, um all jenen Menschen meinen Dank auszusprechen, die mich auf dem langen Weg bis zu diesem Schlusswort begleitet haben: Mein Betreuer Herr Morf gab mir enorme Sicherheit, da ich wusste, dass ich mit meinen Fragen jederzeit zu ihm kommen konnte. Auch meinen Eltern kommt mein herzlicher Dank zu, sie haben klaglos die ewigen Tests und Einmessungen hingenommen, die aus unserem Keller tönten, und haben sowohl meine Freude als auch meine Verzweiflung ausgehalten. Des Weiteren habe ich es der Schlosserei R. Vetterli zu verdanken, dass ich mein Magnetsystem nach Plan habe umsetzen können. Bei der Zehnder Holz Handel AG möchte ich mich für ihren zuvorkommenden und geduldigen Kundenumgang bedanken, nachdem ich bei der Konkurrenz abgewiesen worden war. Für die Inspiration zu meiner Arbeit habe ich Alessio zu danken; einem guten Freund, der das Lautsprecherfieber in mir geweckt hat und mir für diese Arbeit kurzerhand sein Messmikrophon lieh.
Während ich dieses Schlusswort niederschreibe, steht mein selbstgebauter Lautsprecher neben mir und spielt ein Lied von Michael Jackson, und ich bin überzeugt, dass sich alle Bemühungen gelohnt haben.
9. Anhang
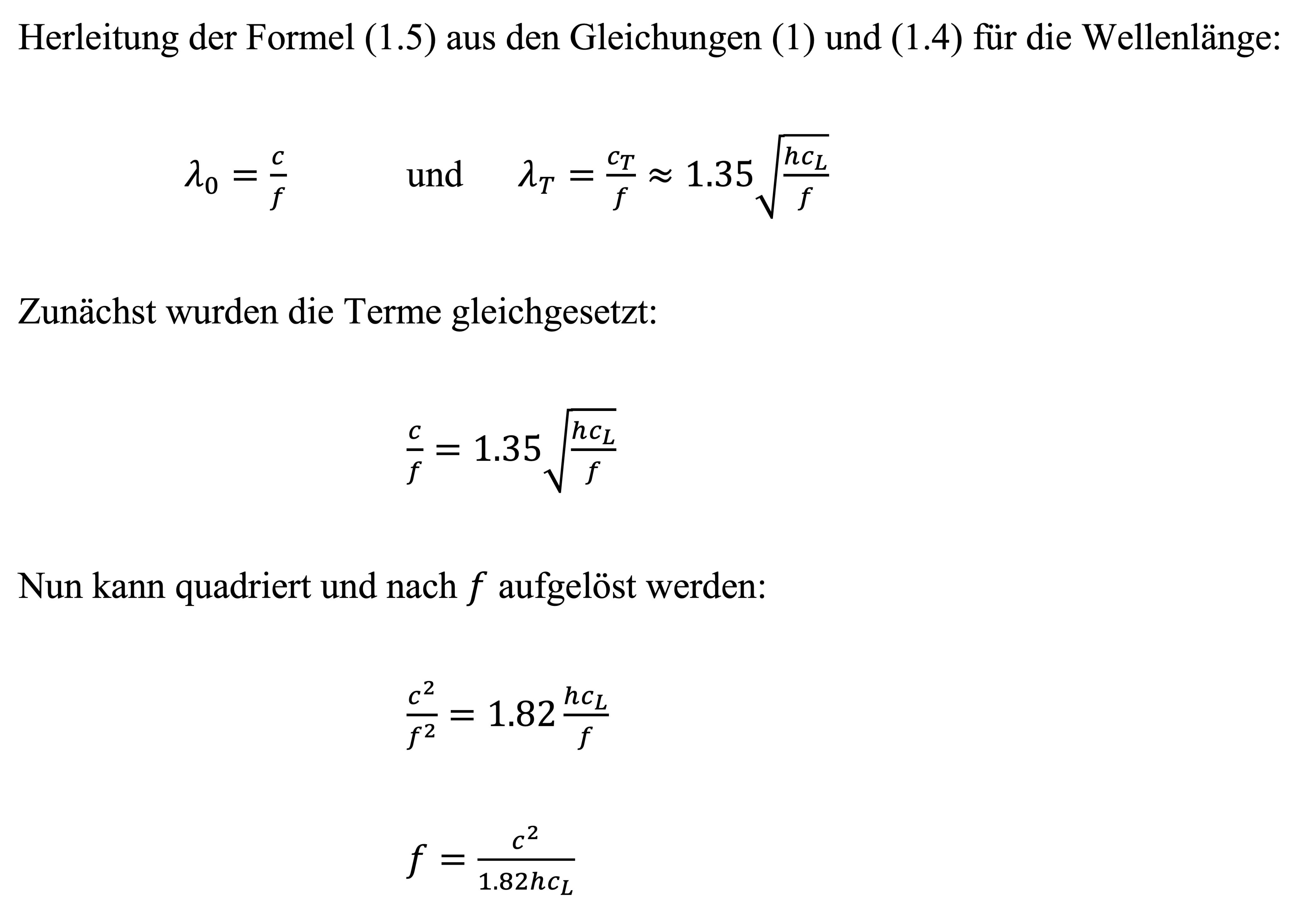
REW-Dateien:
Meine Messdaten sind über DIESEN LINK zugänglich. Zum Öffnen wird die kostenlose Software REW benötigt, die HIER zum Download bereitsteht.
Erste Messergebnisse:
Folgende Messung dient bloss der Belustigung, soll aber auf keinen Fall vorenthalten werden. Sie stellt die Verzerrung des Lautsprechers vor seiner Optimierung dar. Zu sehen sind schwarz die «gesamte harmonische Verzerrung» (Wikipedia, Total Harmonic Distortion, 2019) und braun der Frequenzgang. Man beachte die Verzerrung um 310Hz; sie entspricht ungefähr einem Klirrfaktor von 35%. Zum Vergleich: Bei dieser Frequenz sind Verzerrungen von 0.5% bereits hörbar.
Dementsprechend bescheiden war auch die Wiedergabe in diesem Stadium: Stimmen klangen blechern und Bässe schepperten erbärmlich. Diese Messung erfolgte unter moderater Lautstärke, wenn der Lautsprecher jedoch aufgedreht wurde, blieb von der Musik nicht mehr viel übrig.
Messung 5, Verzerrungen vor der Optimierung
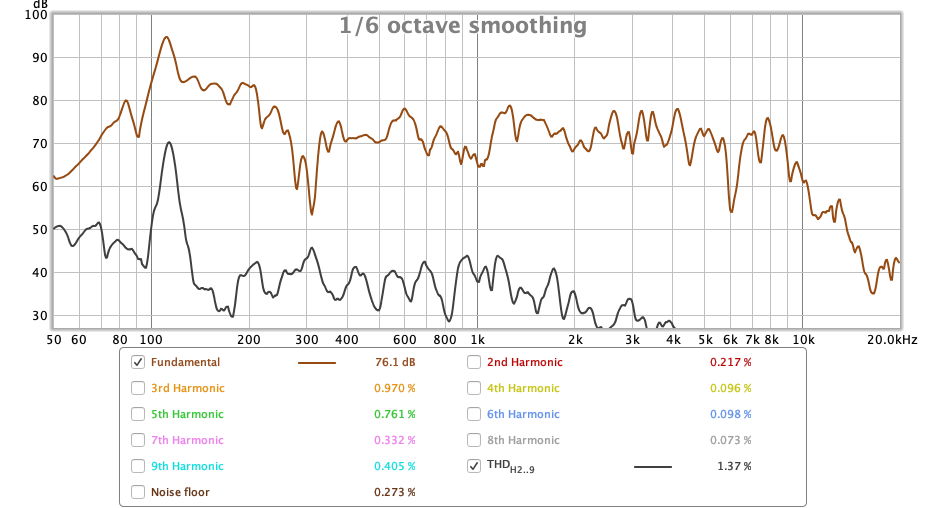
(Quelle: Eigene Messung, exportiert aus REW)
Weiterführende Literatur:
Für die Entwicklung und den Bau von Lautsprechern möchte ich speziell das «Handbuch der Lautsprechertechnik» von Dipl.-Ing. F. Hausdorf empfehlen, es deckt alle wichtigen Formeln zur Berechnung von Lautsprechergehäusen und -weichen ab. Ausserdem erklärt das Buch anschaulich den Aufbau und den Antrieb der gängigsten Lautsprecher.
Als Nachschlagewerk eignet sich der Band «Physik für Ingenieure» von den Herren Hering, Martin und Stohrer.
10. Abbildungsverzeichnis
Schemata:
Schema 1, Verschiedene Wellenformen
Schema 3, Abstrahlung von Körperschall unter- resp. oberhalb der Koinzidenzfrequenz
Schema 4, Elektrodymamischer Antrieb im horizontalen Querschnitt
Schema 7, Messvorrichtung für Impedanzverlauf
Messungen:
Messung 1, Frequenzverlauf, gemessen mit UMIK-1
Messung 2, Verzerrungsgrad meines Lautsprechers
Messung 3, Mein Lautsprecher unter Winkel
Messung 4, Manger-Schallwandler unter Winkel
Messung 5, Verzerrungen vor der Optimierung
Aufnahmen:
Aufnahme 1, Schwingspule auf PET-Träger
Aufnahme 2, Magnetsystem mit Zentriervorrichtung
Aufnahme 3, Gehäuse vor dem Einbau der Membran
11. Literaturverzeichnis
Cremer, L., & Heckl, M. (1996). Körperschall, 2. Auflage. Springer.
Hausdorf, F. (2013). Handbuch der Lautsprechertechnik, 8. Auflage. VISATON.
Hering, E., Martin, R., & Stohrer, M. (2004). Physik für Ingenieure, 9. Auflage. Springer.
Hiebel, H. (2005). Analytische Berechnung der Schallabstrahlung des ebenen Biegewellenwandlers. Technische Universität Graz.
Iris Strassacker Lautsprechershop. (kein Datum). Von https://www.lautsprechershop.de/pdf/manger/manger_chassis.pdf abgerufen
Möser, M. (2015). Technische Akustik, 10. Auflage. Springer.
Mulcah, J. (7. November 2020). REW. Von https://www.roomeqwizard.com abgerufen
PBKreviews. (31. Oktober 2020). Google Pixel 5 5G Disassembly Teardown Repair Video Review. Screen Gap? Abgerufen am 1. November 2020 von https://www.youtube.com/watch?v=PPvlSHyok68&feature=emb_title
Peelen, J. (5. Mai 2016). Own design DML speaker, with sub. Abgerufen am 30. August 2020 von https://www.youtube.com/channel/UCeBox1lGM29f72KL2KrDm7A
Sony. (29. Oktober 2020). Abgerufen am 1. November 2020 von https://www.sony.com
Timmermanns, B. (Juni/Juli 2004). Hobby Hifi.
VISATON. (2019/2020). Lieferprogramm 2020. Haan: VISATON GmbH & Co. KG.
Wikipedia. (16. November 2019). Thiele-Small-Parameter. Abgerufen am 11. November 2020 von https://de.wikipedia.org/w/index.php?title=Thiele-Small-Parameter&oldid=194100624
Wikipedia. (9. November 2019). Total Harmonic Distortion. Abgerufen am 9. November 2020 von https://de.wikipedia.org/w/index.php?title=Total_Harmonic_Distortion&oldid=193886146
Wikipedia. (20. Oktober 2020). Aluminium. Abgerufen am 5. November 2020 von https://de.wikipedia.org/w/index.php?title=Aluminium&oldid=204737912
Wikipedia. (30. Juli 2020). Distibuted mode loudspeaker. Abgerufen am 1. September 2020 von https://en.wikipedia.org/w/index.php?title=Distributed_mode_loudspeaker&oldid=970352493
Wikipedia. (9. März 2020). Hörfläche. Abgerufen am 29. November 2020 von https://de.wikipedia.org/w/index.php?title=Hörfläche&oldid=197609079
Wikipedia. (14. Juli 2020). Klirrfaktor. Abgerufen am 29. November 2020 von https://de.wikipedia.org/w/index.php?title=Klirrfaktor&oldid=201872697
Wikipedia. (8. Juni 2020). Knochenleitung. Abgerufen am 28. August 2020 von https://de.wikipedia.org/w/index.php?title=Knochenleitung&oldid=200766917
Wikipedia. (20. September 2020). Kompressionsmodul. Abgerufen am 11. November 2020 von https://de.wikipedia.org/w/index.php?title=Kompressionsmodul&oldid=194735580
Wikipedia. (25. Oktober 2020). Lautsprecher. Abgerufen am 4. November 2020 von https://de.wikipedia.org/wiki/Lautsprecher
Wikipedia. (22. September 2020). Poissonzahl. Abgerufen am 20. November 2020 von https://de.wikipedia.org/w/index.php?title=Poissonzahl&oldid=203887252
Wikipedia. (14. August 2020). Schallgeschwindigkeit. Abgerufen am 11. September 2020 von https://de.wikipedia.org/w/index.php?title=Schallgeschwindigkeit&oldid=202775653
